In this Technology Insights article, we explore the different technology options for low-emission ammonia production from gas feedstock. What are the different energy, carbon capture, scale and maturity trade-offs that need to be considered? What technology choices are project developers currently making?
In our April episode of Project Features, 8 Rivers joined us to discuss its 8RH2 technology for gas-based hydrogen production with carbon capture rates beyond 99%. As well as the technology itself, we explore the Allam-Fetvedt cycle, the deployment of 8RH2 to produce ammonia in Texas, and 8 Rivers’ future plans.
Meet 8 Rivers to learn about their proprietary 8RH2 technology, which allows for CO2 "capture" in excess of 99% from gas-based ammonia production, and their project based on 8RH2, Cormorant Clean Energy, which will produce 880,000 metric tons of “ultra low carbon” ammonia each year from 2027 in Port Arthur, Texas.
8 Rivers will develop the 880,000 tonnes-per-year production facility in Port Arthur, Texas. Utilizing its proprietary 8RH2 hydrogen production process - where captive CO2 molecules are continuously recycled and utilized - 8 Rivers plans to produce ammonia for local use & export markets, including power generation in South Korea.
As part of a new round of funding announcements, the US Department of Energy will contribute nearly $10 million to three significant ammonia energy initiatives:
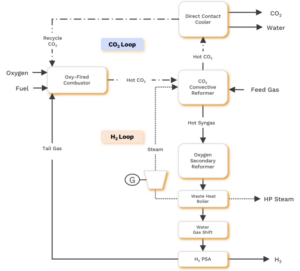
In discussions of carbon capture technology for low-carbon ammonia production, there are two informal rule-of-thumb numbers: 60% and 90%. We know we can capture, at very little additional cost, over 60% of the CO2 from a natural gas-based ammonia plant because this is the process gas (the byproduct of hydrogen production). Many ammonia plants already utilize this pure CO2 stream to produce urea or to sell as food grade CO2. The remaining CO2 emissions are in the much more dilute flue gas (the product of fuel combustion to power the process). For some decades we have assumed we could capture most of this but the lingering question has always been: how much of that flue gas is economically feasible to capture? 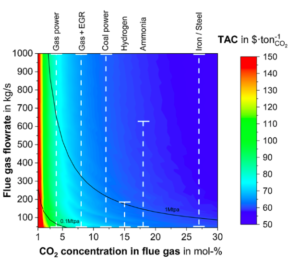A team of researchers at Imperial College London has just published a fascinating study into this question, entitled “Beyond 90% capture: Possible, but at what cost?” The paper quantifies the tipping point — ranging from 90% to 99%, depending on flow rates and concentration — beyond which it is easier to capture CO2 directly from the air than it is to capture more flue gas emissions.
8 Rivers Capital, the developer of “the Allam Cycle, the only technology that will enable the world to meet all of its climate targets without having to pay more for electricity,” unveiled plans in November 2018 for a “billion-dollar clean energy production site” in New Zealand whose outputs are slated to include low-carbon ammonia. That is a sentence with a lot of angles, and unpacking it will take some effort. So let’s start right in with the Allam Cycle.